Tato transformace vychází ze znalosti vlastností pozorovaného signálu – a to zejména statistických informací. Klasická DCT předpokládá stejný rozptyl hodnot v osách X a Y v zdrojovém obraze. Pokud ovšem tento obraz nemá tento rozptyl stejný, ale různý, pak tato DCT transformace zbytečně plýtvá koeficienty a výsledný kompresní poměr by mohl být lepší.

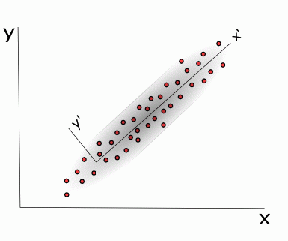
Z obrázku jasně vyplývá vlastní kompresní potenciál KLT, kdy se původní prostor x-y transformoval do prostoru x’-y’ a data v tomto novém prostoru zabírají menší plochu (obdélník) – došlo ke kompresi prostoru – a to nemluvě o dobře komprimovatelných hodnotách v ose y’ která má malý rozsah, a tudíž bude snadno použitelná klasická Huffmanova metoda pro kompresi.
LV transformace (neboli KLT, Karhunen – Loeve transformace, případně Hotellingová transformace) je taková transformace, která dokáže analyzovat vstupní data a optimalizovat bázové vektory klasické DCT transformace tak, že jsou v osách nejvyššího a nejnižšího rozptylu hodnot. Vše názorně vysvětlíme na příkladu.
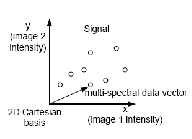
Mějme signál, jehož rozložení význačných bodů je na obrázku. Je vidět, že všechny hodnoty jsou uspořádány kolem jedné přímky, od které mají malou vzdálenost. Tedy říkáme, že tyto data mají v okolí této přímky malou disperzi, a při vhodné volbě bázových vektorů by jsme nemuseli použít signál plného rozsahu xy ale stačil by menší rozsah, jehož hodnoty by byly zahuštěnější. Na to nám poslouží LV.
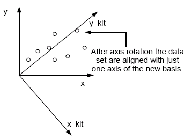
Najdeme si těžiště těchto bodů a to prohlásíme za nový střed souřadného systému. Pak proženeme body algoritmem, který vygeneruje směrnici nejmenší disperze od tohoto středu. Tím dostaneme nový systém, který má jednu osu s velmi malou disperzí, a tato osa může být velmi efektivně komprimována. Pomocí standardní homogenní transformace tyto body transformujeme do nového souřadného systému.
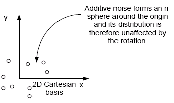
V tomto novém souřadném systému provedeme klasickou DCT, která je však v jedné ose velmi stlačená, díky čemuž můžeme dojít k mnohem vyššímu kompresnímu poměru, než u klasické DCT. Nevýhodou je, že se současně s kompresovanými koeficienty musí přenášet i transformační matice, aby byl proces obousměrný. Proces komprese je značně náročný, ovšem dekomprese je o dost jednodušší. Detailní rozbor algoritmu je následující, a je zřejmý z obrázku:
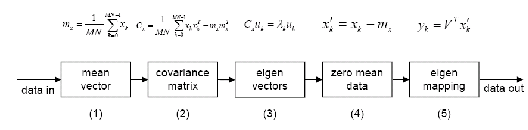
Mějme sadu n sloupcových vektorů x vstupních dat rozměru m. Zavedeme označení, že xi je i-tý vektor a xa je a-tý prvek vektoru.

Tyto vektory poskládejme do matice D následujícím způsobem:
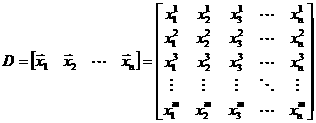
Pokud vynásobíme DDT, vznikne nám matice rozměru n x n, která obsahuje coenergie jednotlivých vektorů vynásobené m. Pokud ovšem provedeme předtím transformační vynásobení maticí A vektory x, bude výsledek formálně následující:
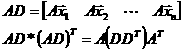
Hledáme matici A takovou, aby výsledek předchozího násobení byl diagonální (všechny energie ve směru osy). Jelikož z matematických pouček plyne, že matice DDT je pozitivně semidefinitní a symetrická (DDT = (DDT)T), dokonce pokud jsou všechny řádky nezávislé, je pozitivně definitní. Tedy platí:
![]()
Z tohoto plyne, že existuje ortogonální matice A taková, že platí AMAT je diagonální matice. Řádkové vektory matice A jsou bázové vektory M. Také plyne že jestli je M pozitivně definitní, potom všechny vektory jsou též pozitivně definitní (jinými slovy, operace nepřevrací prostor).
KLT (Karhunen-Loeve transformace) je význačná právě daným A. Hledaná a minimalizovaná energie jsou jednotlivé prvky na diagonále dělené m. Jelikož KLT se snaží minimalizovat kovarianci, je dobré na počátku zjistit těžiště systému a transformovat vstupní data do tohoto počátku. Tedy na počátku je třeba ještě provést následující úpravy:
Vektor středních hodnot mx matice D je: (m je rozměr matice)
![]()
Pak kovarianční matice se počítá dle vzorce:
![]()
V matici A získáme po provedení všech operací jednotlivé bázové vektory potřebné pro výpočet DCT. Po provedení DCT lze vidět, že koeficienty jsou lépe urovnány, nejsou „rozmazané“ a jsou snadněji komprimovatelné. V obrázkové příloze je příklad vygenerovaných jednotlivých bázových vektorů rozměru 8x8 z daného obrázku a srovnání s klasickými DCT bázovými vektory. Z obrázků je patrné, že vektory KLT jsou různě natočené a na první pohled chaotické.