Vlnková transformace (původně francouzsky ondulette transformation, přeloženo do angličtiny jako kavalet transform – WT) není vlastně jedinou transformací; jde o jistý typ transformací se společnými rysy, vzájemně se lišících podle tvaru zvolené bázové funkce – vlnky. Odlišují se od ostatních transformací především tím, že každá bázová funkce – vlnka – je podporována (tj. má nenulové hodnoty) pouze na konečném časovém intervalu, anebo přinejmenším její hodnoty mimo tento interval jsou zanedbatelně malé. Následkem toho, kterákoli hodnota spektra, založená na využití této vlnky, je ovlivněna pouze odpovídajícím úsekem analyzovaného signálu. Tedy také naopak, vlastnosti, které jsou popsány určitou hodnotou spektra, mohou být vztaženy ke zmíněnému konkrétnímu časovému intervalu, což klasické transformace neumožňují. Vlnkové bázové funkce pokrývají ovšem po částech celý časový rozsah analyzovaného signálu, takže úplná informace je zachována.
ve FT jsou vlastnosti signálu rozprostřeny do celého času a nelze je lokalizovat v t, lokalizace v čase přes translace a v měřítku (frekvence) přes dilatace, rozbíjí signál na změřítkované a posunuté kombinace matčiného waveletu
Wavelet
wavelet - vlnka
K rozkladu signálu se používá waveletů. Postupně se používají změřítkované a posunuté verze „mother wavelet“ od které jsou odvozeny. Umožňují lépe zpracovávat nepravidelné signály a signály s prudkými změnami. Díky postupnému změřítkovávání umožňují i prostorovou lokalizaci vlastností. (U FT je problematické usuzovat na umístění nepravidelností (změn signálu) v časové doméně na základě informací ze spektra, protože obraz určité frekvence je rovnoměrně rozprostřen po celé časové doméně).
Bezeztrátová transformace. Vlnka má konečnou délku.
http://users.rowan.edu/~polikar/WAVELETS/
Multi Resolution Analysis
je konstruovaná tak, aby měla dobré časové rozlišení a špatné frekvenční na vysokých frekvencích a dobré frekvenční a špatné časové na nízkých frekvencích. Hodí se tedy pro signály, které mají krátkodobě rychlé změny a dlouhodobě jsou neměnné (skoro).
Wavelety vychází z principů STFT. Místo okénka jsou bázové funkce waveletu. Místo frekvence se u waveletů používá pojem scale – měřítko. Které udává jak se (ve velikosti) změní matčina vlnka. Druhým parametrem je posun – translation. Měřítko je tím větší, čím je frekvence menší. Jelikož přizpůsobují délku waveletu změřítkováním, umožňují lepší lokalizaci signálu v čase (která je vidět i po tranformaci. Každá frekvence má totiž jinou délku waveletu = okno se mění s frekvencí.
Jádrem výpočtů je mother wavelet – je jich mnoho. Obecně existuje (matematický) popis toho co musí signál splňovat, aby mohl být označen za wavelet. Různé wavelety se (samozřejmě) hodí pro daný signál hůře nebo lépe.
Výpočty začínají pro nejvyšší frekvence (nejkratší zvolený wavelet). Signál je vynásoben z vlnkou a integrován. Postupně se vlnka posunuje po signálu. Po zpracování celé délky signálu je zvětšena hodnota měřítka a opět je proveden výpočet.
Základní vlnku (morlet wavelet) si můžeme představit jako součin gausiánu se sinusem
Na 1D signál dává vlastně 2D odezvu – s osami posun a měřítko. Výsledný bod je tedy vázán na počátek a tvar waveletu a hodnota bodu udává „souhlasnost“ signálu v tomto místě s tvarem tohoto waveletu.
U CWT je možné shift a scaling volit „libovolně“ (a plynule). Rozlišení je tedy možno mít kvalitní (data jsou diskrétní – parametry převodu do WT libovolné. Krok je plunulý / hladký (neboli po jednom kroku)).
DWT počítá výslednou větev (dělí původní signál na) dolní frekvence a horní frekvence. Na větev dolní frekvence se aplikuje tentýž algoritmus. DWPA (Packed Analisys) – je stejná, ale aplikuje tento algoritmus i na větev horní frekvence. Digital znamená, že měřítko a posuv jsou intervaly (obyčejně odvozené od mocnin dvou)
Continuous wavelet transform – CWT.
![]()
Hodnoty spektra
![]() ,
které jsou dvourozměrnou funkcí, jsou dány korelačním intervalem mezi
analyzovaným signálem
,
které jsou dvourozměrnou funkcí, jsou dány korelačním intervalem mezi
analyzovaným signálem
![]() a
bázovou funkcí
a
bázovou funkcí
![]() ,
již je kontrétní vlnka. Charakteristickou vlastností všech vlknových
transformací je, že základní funkční předpis
,
již je kontrétní vlnka. Charakteristickou vlastností všech vlknových
transformací je, že základní funkční předpis
![]() ,
tzv. mateřská vlnka, je stejný pro všechny vektory
,
tzv. mateřská vlnka, je stejný pro všechny vektory
![]() ;
skutečný tvar vlnky však nicméně závisí na obou parametrech. Parametr
a, označovaný jako měřítko (scale), ovládá časovou daleci
funkce (pro a > 1 je vlnka natažena a-krát);
podělení činitelem
;
skutečný tvar vlnky však nicméně závisí na obou parametrech. Parametr
a, označovaný jako měřítko (scale), ovládá časovou daleci
funkce (pro a > 1 je vlnka natažena a-krát);
podělení činitelem
![]() zajišťuje
zachování energie vlnky. Na druhé straně, parametr
zajišťuje
zachování energie vlnky. Na druhé straně, parametr
![]() ovlivňuje
časový posun funkce podél časové osy. Změna tohoto parametru umožňuje
postupně vlnkami určitého konečného trvání pokrýt celý časový rozsah
signálu. Příklad mateřské vlnky
ovlivňuje
časový posun funkce podél časové osy. Změna tohoto parametru umožňuje
postupně vlnkami určitého konečného trvání pokrýt celý časový rozsah
signálu. Příklad mateřské vlnky
![]() a
modifikovaných verzí
a
modifikovaných verzí
![]() a
a
![]() je
zobrazen na .
je
zobrazen na .
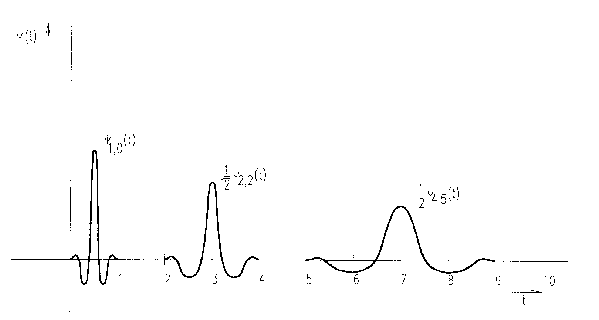
Obr. 1. Mateřská vlnka a její modifikace
Fourierovo spektrum vlnky je podél frekvenční osy stlačeno v poměru měřítka a. Pokut je tvar mateřské vlnky zvolen tak, že i její spektrum má významné hodnoty pouze na konečném intervalu frekvencí , změní se odpovídajícím způsobem mezní kmitočty. Běžné typy vlnek jsou navrženy jako rychle oscilující funkce krátkého časového trvání, tudíž umožňuji detekovat lokální detaily na průběhu signálu.
Discrete wavelet transform - DWT
Nejvýhodnějším způsobem vzorkování je dyadické vzorkování, při němž uzlové hodnoty parametrů jsou dány jako
![]() pro
j,k celé, j≥1
pro
j,k celé, j≥1
Měřítko a je vzorkováno v dyadické (oktávové)
posloupnosti, zatímco časová osa τ je dělena rovnoměrně. Jestliže
je mateřská vlnka
![]() podporována
na
podporována
na
![]() ,
je krok časového posuvu roven délce příslušné vlnky v kterémkoli
měřítku.
,
je krok časového posuvu roven délce příslušné vlnky v kterémkoli
měřítku.
Definiční integrál je nahrazen součtem:
![]()
Kde
![]() jsou
vzorky signálu,
jsou
vzorky signálu,
![]() je
n-tý vzorek k-té posunuté verze diskrétní vlnky, jež je v měřítku
je
n-tý vzorek k-té posunuté verze diskrétní vlnky, jež je v měřítku
![]() ,
N je počet vzorků signálu.
,
N je počet vzorků signálu.
Inversní diskrétní vlnková transformace (IDWT) je lineární kombinací používaných vlnek,
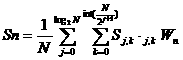
Diskétní vlnková transformace se již prakticky využívá hlavně v oblasti komprese signálu a obrazu. Komprese informací lze provést například tak, že se vynechají koeficienty odpovídající určitým frekvencím. Dojde sice ke ztrátě informace, ale pokud se zvolí koeficienty vhodné, nemusí být změny v signálu poznatelné, obzvláště ne lidským okem nebo uchem.
Dyadické DWT a IDWT lze formulovat v podobě rychlých
algoritmů, realizovaných jistým typem bank filtrů – zrcadlově
kvadratické filtry (Chyba! Nenalezen zdroj odkazů.). Na
obrazku je označen písmenem h hornopropustný filtr, g označuje
dolnopropustný filtr. Výstupní signály těchto filtrů jsou detaily a
aproximace signálu. Symbol
![]() představuje
podvzorkování (oba signály mohou být převzorkovány s polovičním
vzorkovacím kmitočtem, aniž by došlo k aliasing efektu; stačí
tedy zachovat pouze sudé vzorky a vypustit liché.
představuje
podvzorkování (oba signály mohou být převzorkovány s polovičním
vzorkovacím kmitočtem, aniž by došlo k aliasing efektu; stačí
tedy zachovat pouze sudé vzorky a vypustit liché.
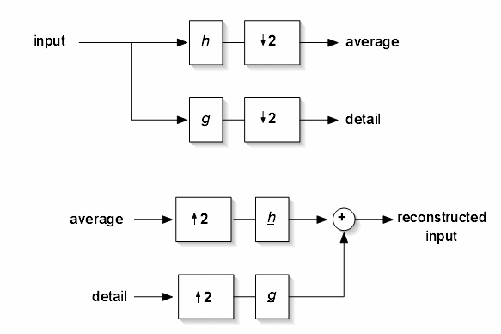
Obr. 2. Dekompozice a rekonstrukce signálu pomocí bank filtrů
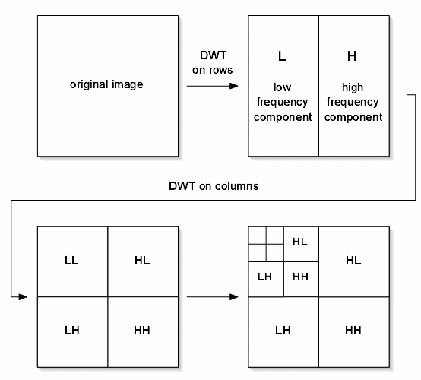
Zatímco jednorozměrná vlnková transformace rozděluje signál do dvou částí (detaily a aproximace), u dvourozměrné vlnková transformace je signál rozdělen do čtyř částí, které si mážeme nazvat (LL, LH, HL, HH). Na Chyba! Nenalezen zdroj odkazů. jsou tyto části jasně patrny.
LL část (low low) nacházející se v levém horním roho obrázku vychází z dolnopropustního filtru z obou směrů (řádky i sloupce) – odtud LL. Ze všech 4 částí se nejvéce blíží původnímu obrazku, proto se nazývá aproximace. Další tři části zobrazují detaily. Pravý horní roh vychází z hornopropustního filtru v horizontálním směru (řádky) a z dolnopropustního filtru ve vertikálním směru (sloupce) – odtud HL. Zbylé dvě části vznikaji podobným způsobem, tak jak je znázorněno v tabulce Tab.1.
|
|
low |
high |
|
low |
LL - aproximace |
HL – vertikální detaily |
|
high |
LH – horizontální detaily |
HH – diagonální detaily |
Tab.1 – rozdělení obrázku při 2D vlnkové transformaci

Obr.3. Jednoúrovňová 2D vlnková transformace, příklad obrázku
Na obrázku 3 je znázorněn příklad dvouúrovňové 2D vlnkové transformace, vznikající rekurzivním průchodem bankami filtrů, což umožňuje jednoduchou realizaci libovolného množství průchodů.

Obr. 4. Příklad dvouúrovňové 2-D vlnkové transformace
Obr. 5. Diagram dvouúrovňové 2D vlnkové transformace
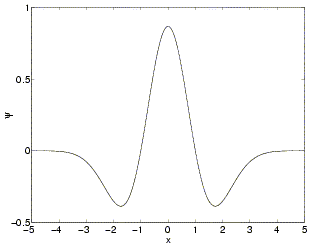
Vlnka Mexikan hat (mexický klobouk nebo také Marrova vlnka) má
tvar druhé derivace průběhu hustoty pravděpodobnosti Gaussova
rozdělení.
Vlastnosti: symetrická, nemá kompaktní nosič, není
ortogonální (nelze použít pro DWT).
![]()
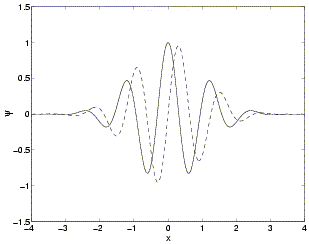
Má tvar komplexní sinusovky modulované Gaussovským oknem. Jedná se o kompromis mezi přesností polohy (lepší je např. Mexikan hat) a frekvenčním rozlišením (FT). Imaginární část je vyznačena čárkovaně.
Vlastnosti: symetrická, komplexní, nemá kompaktní nosič, není ortogonální (nelze použít pro DWT).
![]()
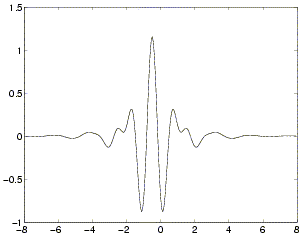
Je definována ve frekvenční doméně, nemá explicitní vzorec pro
vyjádření v čase.
Vlastnosti: symetrická, nemá kompaktní nosič,
ortogonální, je vhodná pro CWT i DWT.
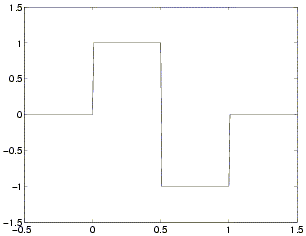
Představuje velmi jednoduchou vlnku, která ale neumožňuje hladkou
rekonstrukci signálu. Bývá často nazývána Daubechies řádu 1.
Vlastnosti: symetrická, má kompaktní nosič, ortogonální, je
vhodná pro CWT i DWT, je jednoduše a efektivně implementovatelná,
nespojitá (to je i přes ostatní výhody velká mínus).
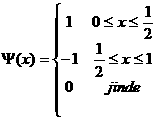
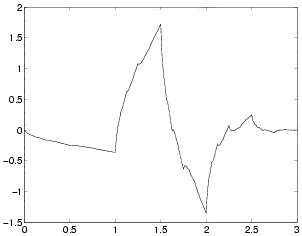
Představuje skupinu vlnek různého řádu N ³1
(N = 1 Haarova vlnka). Nemají, kromě Haarovy, explicitní
vyjádření vlnkové funkce.
Vlastnosti: asymetrická, má kompaktní
nosič délky 2N-1, ortogonální, je vhodná pro CWT i DWT.
Často se provádí výběr vlnky zkusmo nebo intuitivně, nicméně bylo nalezeno několik souvislostí mezi analyzovaných signálem a vhodnou vlnkou:
• Komplexní vlnky jako Morletova detekují dobře oscilace, nejsou vhodné pro detekci osamocených singularit.
• Čistě reálné vlnky s málo oscilacemi dobře detekují špičky a singularity v signálu
• Antisymetrické vlnky jsou vhodné k detekci změn gradientu.
• Symetrické vlnky nezpůsobují fázový posun mezi špičkou, singularitou, oscilaci v signálu a příslušným projevem ve vlnkových koeficientech.
• Pro současnou detekci amplitudy a fáze je nutné použit komplexní vlnku (např. Morletovu)
Vlnková transformace se nejvíce používá při kompresi signálů a obrazu (JPEG2000), ale také při potlačování šumu, detekci hran, detekci objektů, potlačení ozvěny a řadě dalších aplikací.
Úspěšnost nového formátu spočívá především v jeho kompresním algoritmu. Ten je založen právě na vlnkové transformaci.
Algoritmus dosavadního JPEG je založen na tzv. diskrétních kosinových transformacích (Discrete Cosinus Transformation - DCT) využívajících při komprimaci obrázku popisu formou sinusových funkcí. Jejich vlastnosti vyžadují, aby byl obrázek zpracováván po malých čtvercových blocích. Popisy těchto bloků jsou pak v komprimovaném souboru uloženy v pořadí, odpovídajícím rozkladu obrázku směrem shora dolů. To vede k riziku narušení vizuální věrnosti po dekomprimaci (přechody jednotlivých bloků jsou někdy viditelné), nutnosti načtení celého komprimovaného souboru před jeho zobrazením či zpracováním a řadě dalších problémů, jejichž přehled jsme uvedli výše.
Oproti tomu algoritmus založený na vlnkových transformacích pracuje s obrázkem jako celkem a převádí jej na popisy formou vlnových funkcí. Převod je víceprůchodový, počet průchodů určuje kompresní poměr a kvalitu dekomprimovaného obrázku (čím méně průchodů, tím vyšší kompresní poměr, ale tedy i nižší kvalita). Každému průchodu odpovídá zvláštní datový blok komprimovaného souboru. Uvedený princip odstraňuje výše uvedené "čtverečkové přechody" i další problémy a navíc nabízí podstatně flexibilnější zpracování datového toku v komprimovaném souboru.
Walsh-Hadamardova transformace (WHT) představuje nejjednodušší možnou a nejznámější nesinusovou ortogonální transformaci, vyznačující se tím, že její výpočet vyžaduje pouze slučovací operace. Transformace využívá sekvenčně uspořádanou čtvercovou Hadamardovu matici, pro kterou je charakteristické, že její prvky nabývají hodnot +1 nebo -1 a že příslušné˝ řádky a sloupce jsou navzájem ortogonální.
Hadamardova transformace využívá takzvané Hadamardové matice, které se skládají z +1, -1. Jsou definované rekurzivně. Hadamardova matice Hjj je symetrická matice veľkosti jxj, j=2k.
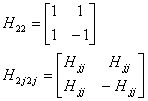
Pro názornost obecná konstrukce Hadamardovy matice [H2N] řáddu 2N vycházející z matice řádu N podle vztahu
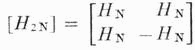
znázorněné na obrázku Obr.11

Obr. 11. Grafické znázornění Hadamardovy matice řádu N=16
( světlá pole= +1, tmavá = -1 ) a) v základním tvaru , b) V uspořádaném tvaru dle rostoucích frekvencí
Jinak inverzní matice k Hadamardovy matici má tvar:
![]()
Hadamardovu transformaci potom definujeme takto:
![]()
inverzní transformace má tvar:
![]()
Hadamardova transformace patří mezi ortogonální transformace.
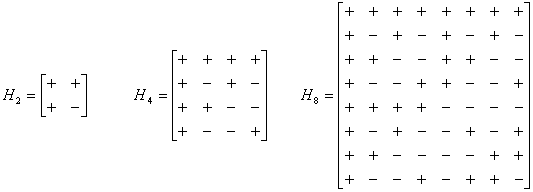
Obr. 12. Hadamardové matice pro k = 1, 2, 3.
Walshova transformace funkce f(x) pro N=2n je definovaná vztahem:

kde bk(z) je k-tý bit čísla z v binární reprezentaci. Transformační matice Walshové transformace je symetrická a ortogonální. Proto tato transformace patří mezi ortogonální transformace.
Inverzní transformace má tvar:
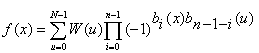
Pro dvojrozměrnou Walshovu a pro její inverzní transformaci platí:
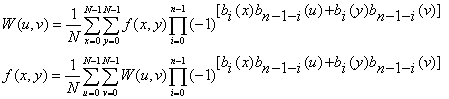
Tyto dvojrozměrné transformace jsou separovatelné, a můžeme je vyjádřit pomocí
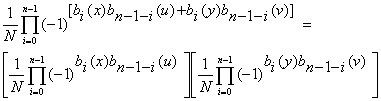
Pro výpočet Walshovy transformace existuje rychlí algoritmus, FWT algoritmus., podobný k FFT algoritmu.Vztahy pro FWT jsou následující:
![]()
![]()
kde M = N/2, u = 0, 1, ..., M-1.
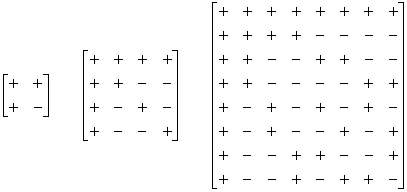
Obr. 13. Koeficienty pro Walshovu transformaci pro n = 1, 2, 3

Obr. 14. Hadamardova transformace obrazu dimenze 8x 8
[1] JAN, Jiří. Číslicová filtrace, analýza a restaurace signálů. Brno : VUTIUM, 2002. 427 s. ISBN 80-214-1558-4.
[2] Úvod do vlnkové transformace [online]. Dostupný z WWW: < http://measure.feld.cvut.cz/usr/staff/smid/wavelets/Wavelet-intro8859.pdf>.
[3] The discrete wavalet transform [online]. Dostupný z WWW: < http://etd.lib.fsu.edu/theses/available/etd-11242003-185039/unrestricted/09_ds_chapter2.pdf>
[4] Filtering banks and discrete wavelet transform [online]. Dostupný z WWW: < http://www.rose-hulman.edu/~brought/Epubs/Imaging/LectNotes4.pdf>
[5] Wavelet-based image processing [online]. Dostupný z WWW: < http://www.uwec.edu/walkerjs/media/WBIP.pdf>
[6] Image coding using wavelet transform [online]. Dostupný z WWW: < http://www.i3s.unice.fr/~barlaud/IP92.pdf>
[7] Wavelet image compression : a heuristic approach to space frequency quantisation [online]. Dostupný z WWW: < http://auc.uow.edu.au/conf/conf03/papers/AUC_DV2003_Tabbara.pdf>
[8] Cache miss analysis of WHT algorithms [online]. Dostupný z WWW: <
www.dmtcs.org/pdfpapers/dmAD0111.pdf
[9] Gábor Blázsovits. DIP - Digital Image Processing, Interaktívna učebnica spracovania obrazu. Bratislava: Katedra aplikovanej informatiky FMFI UK Bratislava