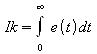
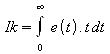 Nevhodné pro záporné e(t). (Záporná hodnota “zlepšuje”
kriterium)
Nevhodné pro záporné e(t). (Záporná hodnota “zlepšuje”
kriterium)Integrální kriteria
Hodnotí velikost (regulační) odchylky. Podle typu se používá pouze odchylka, nebo její absolutní nebo kvadratická hodnota. Lze vážit i časem ve kterém se odchylka objeví.
Výsledkem integrálních kriterií je relativní hodnota – menší hodnota pro lepší přechodný děj (z hlediska daného kriteria). Sama hodnota nic neříká, vždy by měla být vztažena ke stejné soustavě a měla by sloužit ke srovnání navržených regulátorů (pro tuto soustavu).
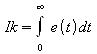
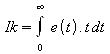 Nevhodné pro záporné e(t). (Záporná hodnota “zlepšuje”
kriterium)
Nevhodné pro záporné e(t). (Záporná hodnota “zlepšuje”
kriterium)
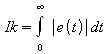
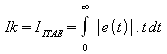 odstranění
předešlé nevýhody absolutní hodnotou.
odstranění
předešlé nevýhody absolutní hodnotou.
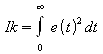
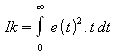 Kvadratické
kriterium – větší pokuta pro hodnoty větší odchylky (než 1).
Kvadratické
kriterium – větší pokuta pro hodnoty větší odchylky (než 1).
Je-li odchylka e(∞) nenulová, pak nemá výpočet moc smysl – záleží na délce časového vektoru pro výpočet (pro t=∞ je výsledek ∞). Proto se tyto hodnotí podle velikosti ustálené odchylky, nebo kombinací ustálené odchylky a výsledkem integrálního kriteria počítaného pro normalizovanou odezvu enorm(t)=e(t)-e(∞).
Nekolného doplněk (Routh-Shurova kriteria stability) – slouží k matematickému výpočtu kvadratického kriteria (neváženého časem).