Funkce slouží k dělení programu na logické části, čímž zlepšuje čitelnost programu. Umožňuje použití stejného kódu v různých místech (za pomoci volání, odskoku do podprogramu). Realizace funkce (tj. instrukce, které ji reprezentují), je v paměti pouze jednou.

Funkce se mohou volat navzájem – rozlišujeme potom funkci volající a funkci volanou. Volající funkce „zavolá“ funkci volanou pomocí instrukce skoku do podprogramu „call“ (na rozdíl od instrukce „prostého“ skoku umístí „call“ na zásobník adresu následující instrukce, protože po ukončení volané funkce se musí pokračovat z místa programu, ze kterého se „odskočilo“). Volaná funkce potom provede svou činnost a je ukončena returnem „return“ zajistí skok na adresu v programu, kterou na zásobník uložil „call“.

Volající a volaná funkce (v jazyce C/C++) sdílí data přes parametry/argumenty a návratovou hodnotu. Parametry jsou uvedeny svým typem a názvem v hlavičce funkce a jsou to lokální proměnné funkce (jejich život končí s instrukcí návratu z funkce). Návratová hodnota je uvedena pouze svým typem a nemá jméno - „zůstane“ po vykonání funkce jako její výsledek a dá se využít ve výrazech jako proměnná daného typu (typ dán návratovou hodnotou). Poté co je použita v daném výrazu (ve kterém je volána funkce) návratová hodnota „mizí“ a již není k dispozici.

Paměťové místo pro parametry funkce i pro návratovou hodnotu je vyhrazeno na zásobníku. Volající i volaná funkce si však musí rozumnět v typu a počtu parametrů. Proto je nutné aby před voláním funkce znal překladač její prototyp (jméno a typy argumentů a návratové hodnoty. Na základě této informace překladač nejen vyhradí správné místo na zásobníku, ale pokud je to nutné, tak provede i konverzi parametru z typu proměnné použité ve volání na typ očekávaný (je-li ve volání funkce, která očekává typ int proměnná typu double, je vyhrazeno místo na int a proměnná typu double je převedena na typ int a uložena do připraveného místa). Pro informování překladače o prototypech funkce slouží uvedení prototypů do hlavičkového souboru, který tímto oznamuje překladači jak má realizovat volání (konverze na typ očekávaný volanou funkcí).

S voláním funkce je spojená režie, spočívající ve „spotřebě“ paměti a času. Paměť je nutná k vytvoření a uložení předávaných proměnných, někdy je ještě před voláním funkce nutné „uklidit“ registry procesoru (uložit je na zásobník), protože volaná funkce je může použít pro své výpočty a tím přemazat v nich uložená data. Po ukončení funkce jsou tato data vrácena zpět do příslušných registrů. Dále je nutné uložit návratovou adresu. Tato manipulace s pamětí a časová režie pro „skoky“ na jiné adresy trvá nějaký čas – časová režie volání funkce.

Jsou funkce, které volají samy sebe (nejčastěji přímo, ale může k tomu dojít i nepřímo (zprostředkovaně)). Používá se při řešení složitějších úloh (například neuronové sítě, expertní systémy), při hledání řešení, kdy se upraví parametry a zavolá se tatáž funkce.

Například výpočet faktoriálu lze vyjádřit funkcí, kdy se ve výpočtu opět vystupuje faktoriál: X! = X (X-1)!, kde výraz (X-1)! se počítá opět podle tohoto vzorce. Tento vzorec se použije pro X > 0, s čímž souvisí ukončovací podmínka (aby se z toho nestal nekonečný algoritmus končící pádem počítače na nedostatek paměti zásobníku). Faktoriál je tak vlastně definován pomocí faktoriálu.

Výhodou rekurze také je, že volání funkce nemusí být provedeno na konci algoritmu ale i na jeho začátku či uprostřed. Část algoritmu se tedy provádí při přímé a část až při zpětné cestě rekurzí. Jako příklad může sloužit tisk hodnot faktoriálu od nuly do daného čísla – u rekurzivního algoritmu faktoriálu se to dá vyřešit tiskem hodnoty po návratu z volání funkce s menším parametrem.
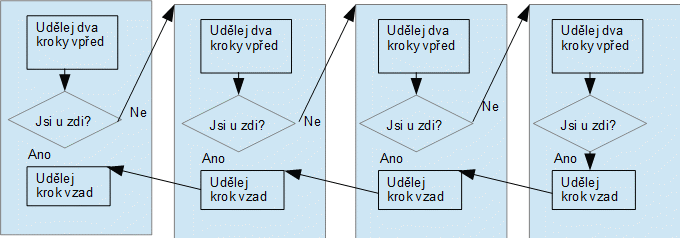
Dalším příkladem je způsob určení poloviny intervalu neznáme-li předem jeho délku (použito v programovacím jazyce Karel). Potom se dá použít rekurzivní algoritmus. Jeho základem je pravidlo, že doprostřed intervalu se dostaneme tak, že na každé dva kroky vpřed uděláme krok vzad. Rekurentní pravidlo společně s podmínkou ukončení lze napsat: Udělej dva kroky a pokud nejsi u zdi, použij tento návod, potom udělej krok zpět. (Průběh algoritmu je na následujícím obrázku, každý obdélník značí jednotlivé volání téže funkce. Pozn. po volání funkce se vracíme na následující část programu).

Nevýhodou rekurzivního volání funkcí je velká paměťová náročnost – při každém volání se vytváří nové lokální parametry, volané a návratové hodnoty. Jelikož se jedná o nestandardně velké požadavky na zásobník, může dojít k jeho přetečení a chybám programu. Překladače proto mají volbu na nastavení velikosti zásobníku.

Většina rekurzivních funkcí se dá přepsat pomocí cyklů – jejich použití je tedy otázkou zhodnocení jejich výhodnosti oproti tomuto řešení. Rekurzi si ukážeme na výpočtu faktoriálu (i když je často zmiňován jako nevhodný příklad použití, jedná se o jednoduchý a známý algoritmus (a z tohoto hlediska je tedy vhodný jako první ukázka této programovací techniky)).

V souboru mainfaktorial.c vypočtěte faktoriál (třemi „způsoby“). Dodržujte přesně požadovaný formát tisku.

0) Načtěte (funkcí scanf) dvě celá čísla oddělená čárkou. První celé číslo je hodnota jejíž faktoriál se bude počítat. Druhé číslo bude nula nebo jedna (udává, zda se provede bod číslo 4 zadání). Pro výpočty využívejte typ long int. Pokud se nenačtou dva parametry, nebo druhé číslo nebude jedna či nula, vypište text „chybne zadani“ a program ukončete s chybovým kódem 1.
1) Napište kód realizující výpočet faktoriálu (nerekurzivní) přímo ve funkci main. Vytiskněte ve funkci main faktoriál zadaného čísla (z bodu 0). Vytiskněte pouze výsledek (číslo) na začátek řádku a odřádkujte. Výpočet a tisk výsledku proveďte pouze je-li parametr pro výpočet správně zadán.
2) Napište funkci (se jménem faktnerek) počítající faktoriál (nerekurzivní). Funkce vrací faktoriál čísla zadaného jako parametr. Pokud parametr nabývá nevhodné hodnoty pro výpočet, vraťte hodnotu nula. Vypočtěte pro zadané číslo faktoriál. Vytiskněte výsledek jako v předchozím bodě.
3) Napište funkci (se jménem faktrek), počítající faktoriál, výpočet realizovaný rekurzivně. Funkce vrací faktoriál čísla zadaného jako parametr. Pokud parametr nabývá nevhodné hodnoty pro výpočet, vraťte hodnotu nula.

4) Využijte funkci z bodu 3 (vytvořte kopii se jménem faktrektisk) tak, aby při jediném jejím volání vytiskla tato funkce tabulku faktoriálů pro čísla od 0 (nuly) do zvoleného čísla. Tuto funkci zavolejte pouze, mělo-li druhé zadané číslo hodnotu 1. Formát tisku je: od začátku řádku je pole desíti znaků do kterých je vytištěna hodnota čísla ze kterého se aktuálně počítá faktoriál (zarovnáno na pravý kraj tohoto pole), potom následuje pole třiceti znaků, do kterého se vytiskne faktoriál aktuální hodnoty (zarovnáno na pravý kraj tohoto pole). Každá dvojice (hodnota + výsledek) má vlastní řádek.

Pokud některá z funkcí ohlásila chybu (vrátila nulu), funkce main vrací hodnotu 2, jinak hodnotu 0.

Jaký je vhodný datový typ pro realizaci proměnných pro výpočet faktoriálu? Jaké jsou rozdíly (výhody/nevýhody použití různých datových typů).

Jaké je maximální číslo (pro zvolený datový typ) jehož faktoriál se dá vypočítat? Navrhněte jak toto číslo zjistit.

Představte si, jaký je rozdíl v použití paměťi (volání funkce, uložení proměnných …) při realizace funkce podle bodu 2 a 3.

Faktoriál je označován „!“ (faktoriál pěti je: 5!=5*4*3*2*1*1= 120 ,10! = 3628800, 1000! = 4,02387260077093773543702433923e+2567). Definice funkce faktoriál je:
i ! je pro kladná i roven součinu (i * (i-1) * (i-2) * … 4 * 3 * 2 * 1).
Pro i=0 je i! = 1.

Zároveň je možné faktoriál definovat i jako rekurentní vztah (v definici se objeví tatáž funkce)
i ! je pro kladná i roven (i * (i-1)! )
pro i = 0 je i! = 1.

Na základě příkladu (example) na adrese http://msdn.microsoft.com/en-us/vstudio/4e2ess30(v=vs.105).aspx (msdn time.h clock) zkuste zjistit kolik času jednotlivé funkce zaberou pro výpočet čísla MAX. (V případě, že je časový interval malý, je vhodné zavolat funkci několikrát a vypočítat průměrný čas).

// crt_clock.c
// This example displays the elapsed time for given program period.
//

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

int main( void )
{
   long    i = 6000000L;
   clock_t start, finish;
   double  duration;

   // Measure the duration of an event.
   printf( "Time to do %ld empty loops is ", i );
   start = clock();
   while( i-- ) 
      ;
   finish = clock();
   duration = (double)(finish - start) / CLOCKS_PER_SEC;
   printf( "%2.1f seconds\n", duration );
}