Návrh regulátoru pomocí kořenového hodografu

Cílem cvičení je provést návrh regulátorů pomocí metody kořenového hodografu. Nejprve se provede rozbor pomocí náčrtu různých variant regulátorů za pomoci kořenového hodografu a následně ověření, nastavení parametrů a zhodnocení pomocí metody gmk v SISOTOOLu. Metoda je vhodná k rychlému srovnání (a výběru kvalitnějšího z) regulátorů..

Zadání

1. Nejprve proveďte „papírově“ rozbor dané úlohy – zhodnoťte slovně možnosti a kvalitu jednotlivých regulátorů (P, I, PI, PD a PID) z hlediska stability, rychlosti a překmitů. Rozbor proveďto pro všechny varianty umístění nul vůči kořenům soustavy.
   Následně pomocí utility SISOTOOL navrhněte postupně tytéž regulátory tak, aby byl systém stabilní a přechodný děj byl co nejkratší. Pro řešení zvolte přenos 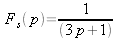. Zkuste předvídat reakce vykreslovaných grafů (kořeny, přechodová charakteristika) při vašich zásazích do parametrů regulátoru.Srovnejte výsledky dosažené v SISOTOOLu s „papírovými“ předpoklady.

2. Sledujte kromě rychlosti také akční zásah, velikost ustálené odchylky a velikost překmitu.

3. Totéž opakujte pro soustavy 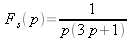a

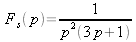
4. Dosažené výsledky srovnejte podle tvaru odezev a pomocí integrálních kriterií s ostatními navrženými regulátory (různými typy i metodami návrhu).

5. Pokuste se odpovědět na následující otázky.

   - Kde musí ležet póly přenosu uzavřené smyčky, aby systém (ne)kmital?

   - Kdy je možné dosáhnout libovolně rychlého přechodného děje a za jakou cenu?.

   - Kdy nelze systém stabilizovat?

   - Jaký vliv má přidání nuly a pólu na tvar kořenového hodografu?

   - Jaký je vliv zesílení regulátoru na kořenový hodograf?

   - jaká je souvislost mezi kořenovým hodografem a frekvenčními charakteristikami?

6. Nyní i v dalších cvičeních si zkuste odpovědět na otázku, která případná změna parametrů soustavy (zrychlení nebo zpomalení) je „výhodnější“. Nebo-li, zda je lepší navrhnout regulátor pro „pomalejší“ variantu soustavy a ten bude fungovat i pro rychlejší soustavu. Nebo zda-li je výhodnější opačná varianta.

Návod řešení

0. Přenos zadané soustavy vytvořte v Matlabu a napište (spusťte) sisotool.

1. Přenos soustavy importujte coby systém G a z menu Analysis vyberte položku Response to step command, která zobrazí nejen odezvu výstupu (modře) ale i odezvu akční veličiny (zeleně).

2. Póly i nuly regulátoru přidáte tak, že dvakrát poklepete na blok C v regulační smyčce a umístíte je podle zvolených hodnot. Orientační umístění je možné přímo graficky myší (symboly x a o v menu).

   Popis metody kořenového hodografu najdete zde.

Pomůcky k řešení

Zadejte v MATLABu Fs (nejprve s jedním pólem). Spusťte SISOTOOL a naimportujte Fs jako soustavu. Zobrazte si odezvu na skok (step) z analýzy. (Modrý průběh je výstup soustavy, zelený průběh je akční zásah).

V části kořenového hodografu se objeví modrá čára zobrazující polohu pólů systému se zpětnou vazbou (Fw). Parametrem na této čáře je zesílení K. (Tj. Měníme-li zesílení v přímé větvi regulovaného obvodu (na místě regulátoru), mění se poloha pólů zavazbeného systému tak, že se pohybují po vyznačených čarách). Aktuální poloha pólů je označena čtvercem – v jednom čase může být nastaveno pouze jedno K, tj. Na každé čáře je vybrán jeden bod – pól. Příslušné K je zobrazeno nad kořenovým hodografem. Vybereme-li pól na jedné čáře, zároveň volíme zesílení K, a tudíž i polohu pólů na ostatních čarách. Čáry nazýváme větvemi hodografu. Jedna větev připadá na jeden řád (jmenovatele) uzavřeného systému.

Chceme-li dosáhnout rychlé regulace – odezvy, musíme volit polohu pólu co nevíce vlevo. Všiměte si, že volba polohy pólu je totožná s volbou zesílení regulátoru – to znamená, že zvolíme-li zesílení, dopočítají se póly pro jednotlivé větve, zvolíme-li umístění pólu na jedné větvi, dopočítá se zesílení a ostatní póly. Současně s posunem dominantního pólu vlevo se zrychluje odezva (pro účely hodnocení rychlosti volme jako čas ustálení takový čas, že přechodová charakteristika dosáhne pásma +- 5%ustálené hodnoty a z něj již nevyjde). S rychlostí odezvy však narůstá velikost akčního zásahu. Omezíme-li přípustnou velikost akčního zásahu na 2 (což je v našem případě pětinásobek hodnoty ustálené hodnoty akčního zásahu) potom nám vyjde dosti špatná přechodová charakteristika. (Omezení hodnoty akčního zásahu je voleno jako příklad, ale v praxi je vždy nutné počítat s omezenou hodnotou akčního zásahu). Dalším hodnoceným parametrem výsledného průběhu může být například maximální hodnota překmitu (Pro náš příklad si například povolíme maximálně 20%). Tyto povolené hodnoty mohou pracovat spolu, nebo proti sobě a potom je nutno volit kompromisní řešení. Tímto jsme vlastně provedli rozbor pro volbu regulátoru typu P.

Jako druhý regulátor si vyberme PD. V tomto případě můžeme do kořenového hodografu doplnit jednu nulu. Po jejím doplnění se nám graf překreslí a zobrazí se čáry možného výskytu pólů pro soustavu s tímto regulátorem pro všechna K (PD regulátoru s danou nulou). Na těchto čarách opět volíme jedno konkrétní K. Nulu je možné umístit dvěma způsoby. Srovnejte obě možná řešení a lepší z nich srovnejte s regulátorem P, zda došlo ke zlepšení či zhoršení.

Nevýhodou předchozích řešení je nenulová ustálená odchylka (pro jaká K se odchylka zmenšuje?). Nulovou ustálenou odchylku nám zajistí až integrační složka v regulátoru (není-li v soustavě). Pól v počátku zadávejte kliknutím na regulátor, kde v sekci poles zadáte hodnotu 0 – tj. Pól v nule. (Zadáním pomocí myši se většinou do počátku přesně netrefíte). Opět se vykreslí čáry hodografu, které zobrazují putování pólů při změně zesílení K (tentokráte však již pro I regulátor). Maximální poloha voleného pólu přenosu řízení by mohla být u levého pólu původní soustavy. Ovšem k němu patří odpovídající pól na druhé větvi a ten je umístěn nevýhodně. Zároveň je to pól dominantní (pól, který určuje rychlost – ten který je nejvíce vpravo). Zapamatujte si hodnoty času odezvy a snažte se posouvat póly po kořenovém hodografu. Povolíme-li si překmit, můžeme umístit póly i do části mimo reálnou osu. Potom bude odezva kmitavá. Čím více od reálné osy - tím kmitavější. (pomocí volby grid pravého tlačítka lze v kořenovém hodografu zobrazit přímky konstantního ksí – parametru kmitavého článku druhého řádu, kterým je určena velikost překmitu). Za cenu překmitu získáme zrychlení odezvy.

Dále můžeme pokračovat PI regulátorem, který má pol v počátku (jako I regulátor), jednu nulu – máme opět více možností jejího umístění a parametrem na čarách je opět zesílení K.

PID regulátor má pól v počátku a možnost umístit dvě nuly. Rozbor možných kombinací umístění nul je u něj tedy složitější. Z možných řešení vybereme opět to nejlepší a to srovnáme s předchozími řešeními.

U regulátorů s derivační složkou (PD, PID) je nutné si uvědomit, že u reálného regulátoru musíme ještě přidat realizační konstantu. Pokud je dostatečně malá, potom sice významně ovlivňuje tvar hodografu ale pro „rozumná“ zesílení nemá na výsledné průběhy vliv – ověřte toto tvrzení.

Obdobně proveďte rozbor pro ostatní systémy.

Poslední změna 2008-04-01